中２で全国統一高校生テスト(全学年統一部門)を受けてみた：数学ⅠA・数学ⅡB　中高一貫校

人気記事TOP5

上の子は中２で全国統一高校生テストの全学年統一部門を受けましたが、決して学力に自信があるというわけではなく、東進ハイスクールに在籍しているため、受けざるを得なかったという後ろ向きな理由からです。
中高一貫校に通う後ろ向きな中学２年生が、全国統一高校生テストでどのくらいの結果を出せるのか、ご参考になれば幸いです。

全国統一高校生テストは東進ハイスクールが年２回開催している全国規模の無料の模試です。
全国統一高校生テストは高１部門、高２部門、全学年統一部門の３部門に分かれていますが、今回は全学年統一部門を受験しています。

東進ハイスクール・東進衛星予備校資料請求はこちらからどうぞ

全国統一高校生テストとは
全国統一高校生テスト全学年統一部門の結果
1. 中2　６月　全国統一高校生テスト全学年統一部門
2. 中2　１１月　全国統一高校生テスト全学年統一部門
  1. 数学ⅠA
  2. 数学ⅡB
まとめ

全国統一高校生テストとは

「独立自尊の社会・世界に貢献する人財を育成する」という教育目標を掲げる東進は、住んでいる地域や経済的な事情に関係なく、すべての高校生に学力向上の機会を広く提供するため、「全国統一高校生テスト」を年に２回実施し、いずれも無料で招待しています。またこのテストにより、日本全国に埋もれている優れた才能を発掘し、その力を存分に伸ばしていくことにより、将来、世界をリードする新しい日本を築いていく人財が次々と育ってくれることを願っています。

「全国統一高校生テスト」は、単に点数や順位、偏差値を出すなどの学力を測るだけのテストではなく学力を伸ばすためのテストです。これまでの努力の成果が分かるとともに、自分の弱点ややるべき課題が明確になり、学力を伸ばす多くのヒントが得られます。また、成績優秀者を対象に全国の精鋭たちが競い合い、高め合う場として決勝大会を開催。決勝大会成績優秀者はその栄誉を称え、表彰します。

さらに、世界にはばたくリーダー育成を支援するために海外大学留学支援制度を実施しています。
「全国統一高校生テスト」の決勝大会で特に優秀な成績を収めた方を対象に、1人当たり総額38万ドル（4年間累計）を給付。毎年各学年最大10名の留学を支援します。海外大学での体験は多様な人的交流を促し、人間力を高め、国際社会で活躍する人財を生み出す原動力となります。

「全国統一高校生テスト」の受験が、まだ見ぬ全国のライバルたちと出会い、ともに切磋琢磨し、学力向上や志望校合格とその先の志の実現に向けた第一歩となることを期待しています。

東進ハイスクール・東進衛星予備校資料請求はこちらからどうぞ

大学入学共通テストと同じ出題形式・レベルの本番レベル模試

「全国統一高校生テスト」は実際の大学入学共通テストと同じレベル・出題形式の「本番レベル模試」。さらに統一実施日に試験会場での厳正実施により学力を正確に測ります。本番の難易度や科目・分野ごとの得意不得意を知り、志望校合格まであと何点必要かわかります。

試験実施から中5日で成績表を超スピード返却

模試受験後は復習がとても重要です。受験本番までの限られた時間を有効活用するために、成績表(君だけの診断レポート)は、試験実施から最短中5日でスピード返却。問題を解いたときの感覚と記憶が残っているうちに復習できるため、学習効果がぐっと高まります。

君だけの診断レポート(成績表)で今やるべき課題が明確になる

志望校の合格可能性や偏差値を示すのはもちろんのこと、全科目の全設問について、単元・ジャンル別に君の学力を徹底診断。君の克服すべき課題を明確に示し、今やるべきことがはっきり分かります。合格者との成績データ比較により現在位置がわかり、今後の目標得点を定めることが可能です。

東進ハイスクール・東進衛星予備校の資料請求をします

全国統一高校生テスト全学年統一部門の結果

中2　６月　全国統一高校生テスト全学年統一部門

６月は国語も一緒に受験したので国語の結果も掲載します。英語は未受験です。
現代文は中学受験のテクニックである程度の点数がとれますが、古文漢文は中２では太刀打ちできませんね。ほぼ勘で解いたと思います。
数学は東進のおかげで中２の段階で数１Aと数２Bは一通り終えていますが、まだまだ基礎が抜けている状態です。

国語

現代文ー論理的文章
全体把握が不十分のようです。本文全体の把握が不十分です。部分的に難しいことが書かれていても、本文全体の関係を捉えれば、理解できることも多くあります。演習を積んで、読解力を伸ばしていきましょう。
現代文ー文学的文章
全体を押さえて読めています。レベルの高い問題にチャレンジできます。文学的文章の代表である小説の読み取りができています。今後、心情表現のわかりにくい小説や、随筆や詩などの問題でも得点できるよう、いろいろなタイプの問題にも取り組んでいきましょう。
古文
古文を正確に読むことができていないようです。わかる単語をつないで、なんとなく読んでいるところがあるようです。それでは正しく読めません。まずは重要古語や、古典文法をしっかり覚え、知識を駆使して読むことを心がけましょう。
漢文
漢文の勉強が進んでいないようです。漢文を短時間で読み取るためには、基礎となる漢文の力があることが前提です。まずは重要な句法と語彙の知識を短期集中で身につけましょう。そうすれば、今までただの漢字の羅列に見えていたものが、意味をもった文章になり、勉強も楽しくなりますよ。

数学Ⅰ

数と式、集合と論理、図形と計量
絶対値を含む式の計算、論理と集合の理解、三角比の定義・定理などの基本などがまだ十分に理解できていないようです。教科書に書いてある基本事項の徹底理解に努めましょう。
２次関数、データの分析
与えられた表からの立式、２次方程式の最大値、データの分析や箱ひげ図の読み取りなどの理解に曖昧な個所が残っているようです。２時間数の位置関係、箱ひげ図や散布図の特徴を読み取る力をしっかりと身につけましょう。
整数の性質
不定方程式の整数解の考え方の理解が不十分です。不定方程式の整数解の基本的な考え方について教科書の見直しをしっかりと行いましょう。
図形の性質
図形の中で用いることのできる定理や性質の理解が不十分です。図形の中で用いることのできる定理や性質をまず理解することから始めましょう。

数学Ⅱ

指数関数・対数関数、複素数と方程式、式と証明
対数を含む関係式、恒等式の性質、背理法での証明がしっかりと身についています。問題演習を通して、より複雑な式変形や計算にもチャレンジしていきましょう。
三角関数、微分法
三角関数で表された関数の３次関数への置き換え、最大値・最小値や方程式の解の個数、グラフの概形・面積を求める家庭に曖昧な箇所があるようです。どこでつまずいたかを把握したうえで、間違えた箇所の徹底理解に努めましょう。
数列
誘導に従って数列を理解、漸化式をつくる過程に曖昧な箇所があるようです。どこでつまずいたかを把握した上で、間違えた箇所の徹底理解に努めましょう。
ベクトル
基本的なベクトルの性質の理解が不十分です。ベクトルの性質を演習を繰り返し、定着させましょう。

中2　１１月　全国統一高校生テスト全学年統一部門

１１月は数学のみの受験で、英語、国語は未受験です。
数学は５月と比較して得点は伸びましたが、全国平均も伸びているのでほぼ、全国平均と変わらず。

数学ⅠA

項目	得点率	評価	処方箋
①数と式、集合と論理、図形と計量	73.3%	絶対値を含む不等式、集合の包含関係・共通部分、三角比の定義、正弦定理や余弦定理の活用などの基本でまだ定着していない箇所があります。	各分野の基本で理解が不十分だった箇所について、解答解説を確認し、理解を確実なものにしましょう。
②2次関数、データの分析	60.0%	2次関数のグラフ概形・頂点の移動、ヒストグラムなどの図の読み取り、四分位数などの変化、相関係数計算などの理解に曖昧な箇所が残っているようです。	2次関数の位置関係、箱ひげ図や散布図の特徴を読み取る力をしっかりと身に付けましょう。
④整数の性質	45.0%	不定方程式の整数解の考え方の理解が不十分です。	不定方程式の整数解の基本的な考え方について教科書の見直しをしっかりと行いましょう。
⑤図形の性質	45.0%	図形の中で用いることのできる定理や性質の理解が不十分です。	図形の中で用いることのできる定理や性質をまず理解することから始めましょう。

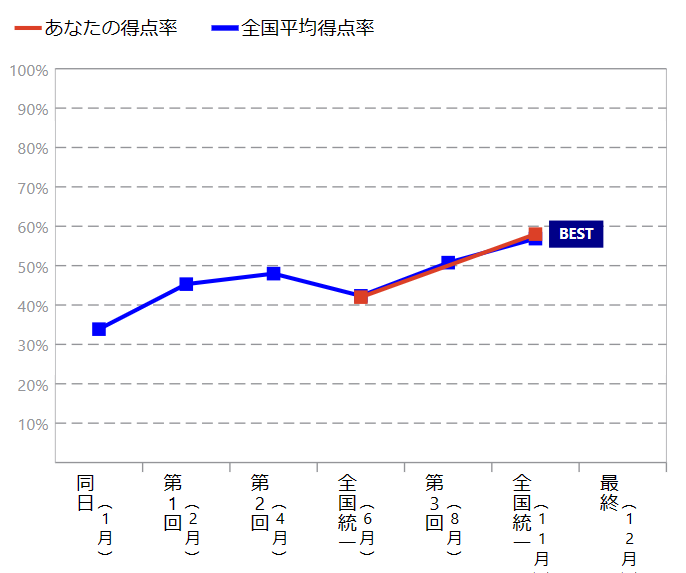
数ⅠAの得点率は６月、１１月ともにほぼ全国平均と同じでした。

数学ⅡB

項目	得点率	評価	処方箋
①複素数と方程式、三角関数	70.0%	方程式との解の意味、３次方程式と２次方程式の共通解、三角関数の合成・式変形の理解に曖昧な箇所があるようです。	どこでつまずいたかを把握した上で、間違えた箇所の徹底理解に努めましょう。
②微分・積分	73.3%	定積分の形で定義された関数について、接線・増減・グラフの概形・2つの関数のグラフで囲まれる図形の面積を求める過程に曖昧な箇所があるようです。	どこでつまずいたかを把握した上で、間違えた箇所の徹底理解に努めましょう。
④数列	40.0%	基本的な数列、漸化式の理解が不十分です。	典型的な数列、漸化式の復習に加えて、人に数列の状況が説明できるようにしましょう。
⑤ベクトル	30.0%	基本的なベクトルの性質の理解が不十分です。	ベクトルの性質について演習を繰り返し、定着させましょう。